Binary Search Trees
Binary search trees (BST) are binary trees where values are placed in a way that supports efficient searching. In a BST, all values in the left subtree value in current node < all values in the right subtree. This rule must hold for EVERY subtree, ie every subtree must be a binary search tree if the whole tree is to be a binary tree. The following is a binary search tree:
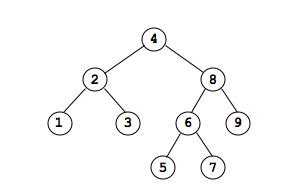
The following is NOT a binary search tree:
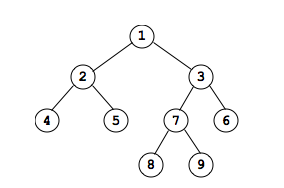
A binary search tree allows us to quickly perform a search on a linking structure (under certain conditions). To find a value, we simply start at the root and look at the value. If our key is less than the value, search left subtree. If key is greater than value search right subtree. It provides a way for us to do a "binary search" on a linked structure which is not possible with a linear linked list. Note that we will never have to search the subtrees we eliminate in the search process... thus at worst, searching for a value in a binary search tree is equivalent to going through all the nodes from the root to the furthest leaf in the tree
Insertion
To insert into a binary search tree, we must maintain the nodes in sorted order. There is only one place an item can go. Example Insert the numbers 4,2,3,5,1, and 6 in to an initially empty binary search tree in the order listed. Insertions always occur by inserting into the first available empty subtree along the search path for the value:
Insert 4:

Insert 2: 2 is < 4 so it goes left
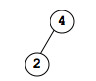
Insert 3: 3 is less than 4 but more than 2 so it goes to left of 4, but right of 2
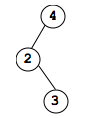
Insert 5: 5 is > 4 so it goes right of 4
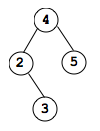
Insert 1: 1 is < 4 so it goes to left of 4. 1 is also < 2 so it goes to left of 2
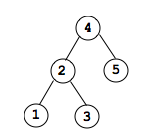
Insert 6: 6 is > 4 so it goes to right of 4. 6 is also > 5 so it goes to right of 5
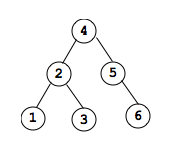
Removal
In order to delete a node, we must be sure to link up the subtree(s) of the node properly. Let us consider the following situations.
Suppose we start with the following binary search tree:
Suppose we were to remove 7 from the tree. Removing this node is relatively simple, we simply have to ensure that the pointer that points to it from node 6 is set to nullptr and delete the node:
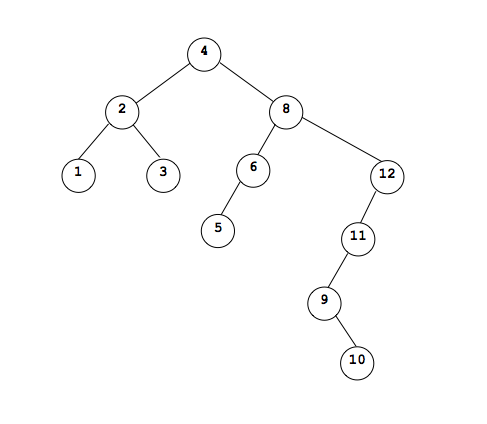
Now, Lets remove the node 6 which has only a left child but no right child. This is also easy. all we need to do is make the pointer from the parent node point to the left child.
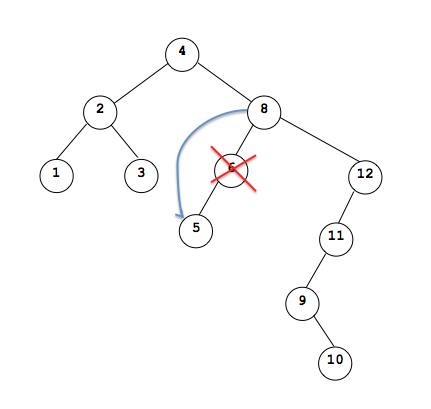
Thus our tree is now:
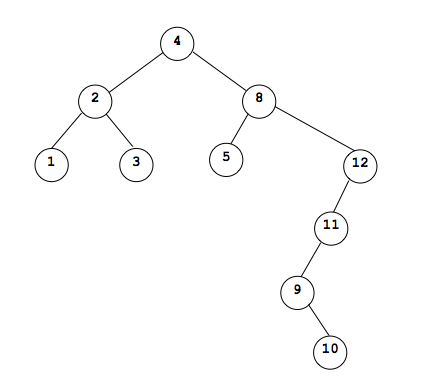
Now suppose we wanted to remove a node like 8. We cannot simply make 4 point to 8's child as there are 2 children. While it is possible to do something like make parent point to right child then attach left child to the left most subtree of the right right child, doing so would cause the tree to be bigger and is not a good solution.
Instead, we should find the inorder successor (next biggest descendent) to 8 and promote it so that it replaces 8.
The inorder successor can be found by going to the right child of 8 then going as far left as possible. In this case, 9 is the inorder sucessor to 8:
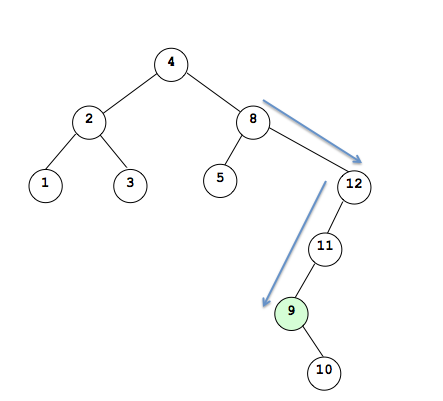
The inorder successor will either be a leaf node or it will have a right child only. It will never have a left child because we found it by going as far left as possible.
Once found, we can promote the inorder successor to take over the place of the node we are removing. The parent of inorder successor must link to the right child of the inorder succesor.
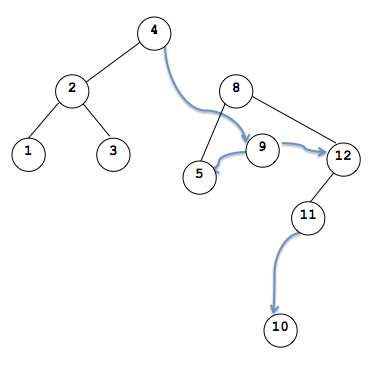
In the end we have:
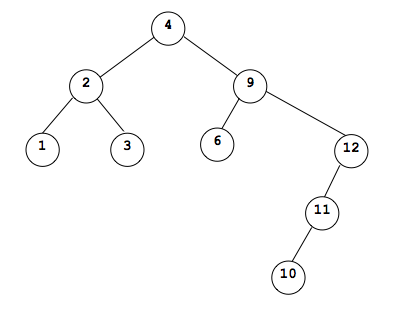
Traversals
There are a number of functions that can be written for a tree that involves iterating through all nodes of the tree exactly once. As it goes through each node exactly 1 time, the runtime should not exceed O(n)
These include functions such as print, copy, even the code for destroying the structure is a type of traversal.
Traversals can be done either depth first (follow a branch as far as it will go before backtracking to take another) or breadfirst, go through all nodes at one level before going to the next.
Depth First Traversals
There are generally three ordering methods for depth first traversals. They are:
preorder
inorder
postorder
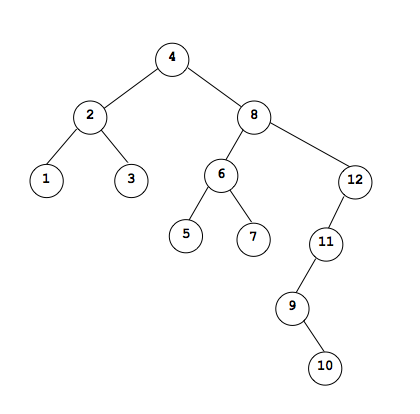
In each of the following section, we will use this tree to describe the order that the nodes are "visited". A visit to the node, processes that node in some way. It could be as simple as printing the value of the node:

Preorder traversals
visit a node
visit its left subtree
visit its right subtree
4, 2, 1, 3, 8, 6, 5, 7, 12, 11, 9, 10
Inorder traversals:
visit its left subtree
visit a node
visit its right subtree
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
Notice that this type of traversal results in values being listed in its sorted order
Postorder traversals:
visit its left subtree
visit its right subtree
visit a node
1, 3, 2, 5, 7, 6, 10, 9, 11, 12, 8, 4
This is the type of traversal you would use to destroy a tree.
Breadth-First Traversal
A breadfirst traversal involves going through all nodes starting at the root, then all its children then all of its children's children, etc. In otherwords we go level by level.
Given the following tree:

A breadthfirst traversal would result in:
4, 2, 8, 1, 3, 6, 12, 5, 7, 11, 9, 10
Last updated